In the 13th century in Italy, Leonardo of Pisa or better known as Fibonacci, was the most talented western mathematician in the middle ages. He was the son of a customs officer and as a child, he travelled to North Africa with his father, where he learned about Arabic mathematics. When he returned to Italy, he helped spread this knowledge throughout Europe, bringing reforms in European mathematics, which had not been active for centuries during the Dark Ages.
Specifically, in 1202, he wrote a very influential book called ‘Liber Abaci’ (‘Book of Calculation’), in which he promoted the use of numerical systems and the advantages of this system to Hindu-Arabs. Fibonacci explains the advantages to merchants and mathematicians when compared to the Roman numerals used in Europe. Although the advantages are clear, the use of the system in Europe is slow (this is after the Crusades against Islam, the time in which Arabic language is viewed with great suspicion), and Arabic numbers were forbidden in the city of Florence in 1299 as Arabic numerals seem to be easier to forge when compared to Roman numerals. However, rational thinking could overcome anything. The new system was adopted throughout Europe in the 15th century, making the Roman system obsolete. The ‘Horizontal bar’ notation for fractions was also first used in this work (although the Arab practice is to place fractions on the left of the integer).
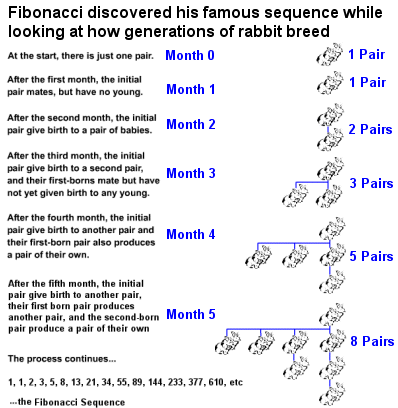
Fibonacci is extremely well known, especially after introducing a sequence of certain numbers to Europe, which has since been called the Fibonacci Numbers or Fibonacci Sequences. He encountered the sequence – the first repetitive sequence of numbers known in Europe – while considering the practical issue in ‘Liber Abaci’ involving hypothetical population growth based on the ideal assumptions. He said that after every monthly generation, the number of pairs of rabbits increased from 1 to 2 to 3 to 5 to 8 to 13, and so on, and identifying how the sequence develops by adding two previous terms (in mathematical terms, Fn = Fn − 1 + Fn − 2), a sequence that can in theory evolve forever.
The actual sequence has been known by Indian mathematicians since the 6th century, consisting several interesting mathematical properties, and many of the implications and related sequences are still unknown for centuries even after Fibonacci’s death. For example, the sequence reinforces itself in some surprising way: every third F number divided by 2 (F3 = 2), each fourth F number divided by 3 (F4 = 3), each fifth F number divided by 5 (F5 = 5), every sixth F number is divided by 8 (F6 = 8), every seventh number F is divided by 13 (F7 = 13), and so forth. The sequence series is also seen when a flowering plant species has the number of petals in the Fibonacci sequence; Pineapple spiral arrangement occurs in 5s and 8s, pinecones in 8s and 13s, and sunflower seeds are headed in 21s, 34s, 55s or higher terms in sequence and so on.
